Integral formulations of volumetric transmittance
Abstract
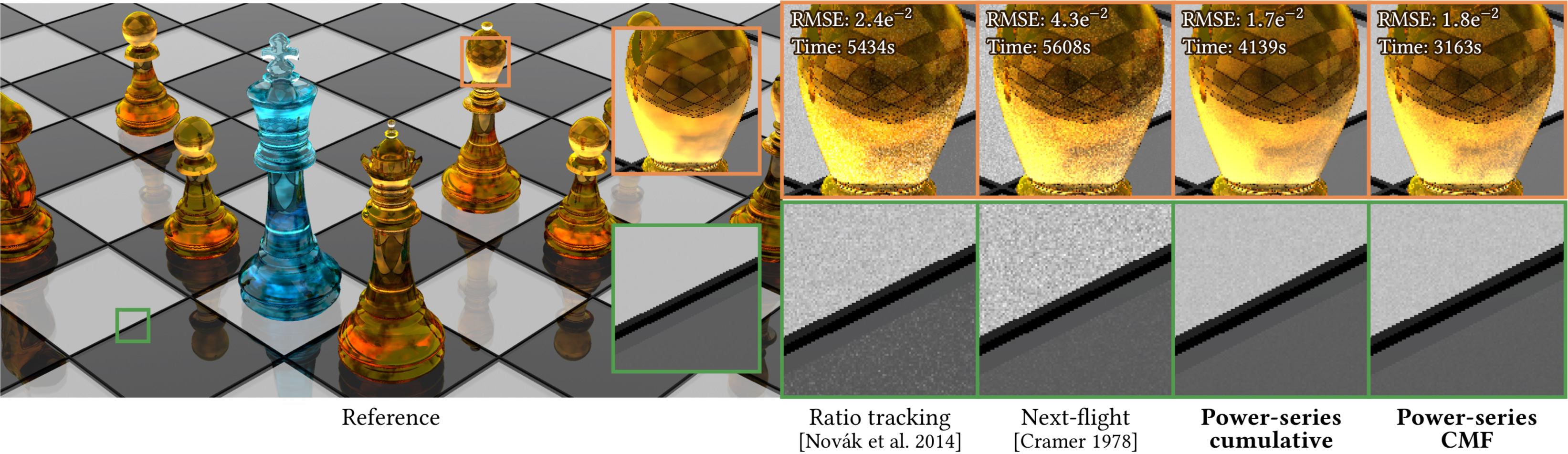
Computing the light attenuation between two given points is an essential yet expensive task in volumetric light transport simulation. Existing unbiased transmittance estimators are all based on "null-scattering" random walks enabled by augmenting the media with fictitious matter. This formulation prevents the use of traditional Monte Carlo estimator variance analysis, thus the efficiency of such methods is understood from a mostly empirical perspective. In this paper, we present several novel integral formulations of volumetric transmittance in which existing estimators arise as direct Monte Carlo estimators. Breaking from physical intuition, we show that the null-scattering concept is not strictly required for unbiased transmittance estimation, but is a form of control variates for effectively reducing variance. Our formulations bring new insight into the problem and the efficiency of existing estimators. They also provide a framework for devising new types of transmittance estimators with distinct and complementary performance tradeoffs, as well as a clear recipe for applying sample stratification.
Downloads and links
- paper (PDF, 11 MB)
- slides – from the conference presentation (KEY, 43 MB)
- slides – from the conference presentation (PDF, 19 MB)
- presentation video (MP4, 36 MB)
- supplemental results – interactive image comparisons and error data
- code – C++ implementation of various transmittance estimators
- citation (BIB)
Media
Presentation video
BibTeX reference
@article{Georgiev:2019:TransmittanceFormulations,
author = {Iliyan Georgiev and Zackary Misso and Toshiya Hachisuka and Derek Nowrouzezahrai and Jaroslav K\v{r}iv\'{a}nek and Wojciech Jarosz},
title = {Integral formulations of volumetric transmittance},
journal = {ACM Transactions on Graphics (Proceedings of SIGGRAPH Asia)},
volume = {38},
number = {6},
year = {2019},
month = nov,
keywords = {participating media, transmittance, null collision, null scattering, stochastic sampling, Monte Carlo integration}
}