Marginal multiple importance sampling
Abstract
Multiple importance sampling (MIS) is a powerful tool to combine different sampling techniques in a provably good manner. MIS requires that the techniques' probability density functions (PDFs) are readily evaluable point-wise. However, this requirement may not be satisfied when (some of) those PDFs are marginals, i.e., integrals of other PDFs. We generalize MIS to combine samples from such marginal PDFs. The key idea is to consider each marginalization domain as a continuous space of sampling techniques with readily evaluable (conditional) PDFs. We stochastically select techniques from these spaces and combine the samples drawn from them into an unbiased estimator. Prior work has dealt with the special cases of multiple classical techniques or a single marginal one. Our formulation can handle mixtures of those.
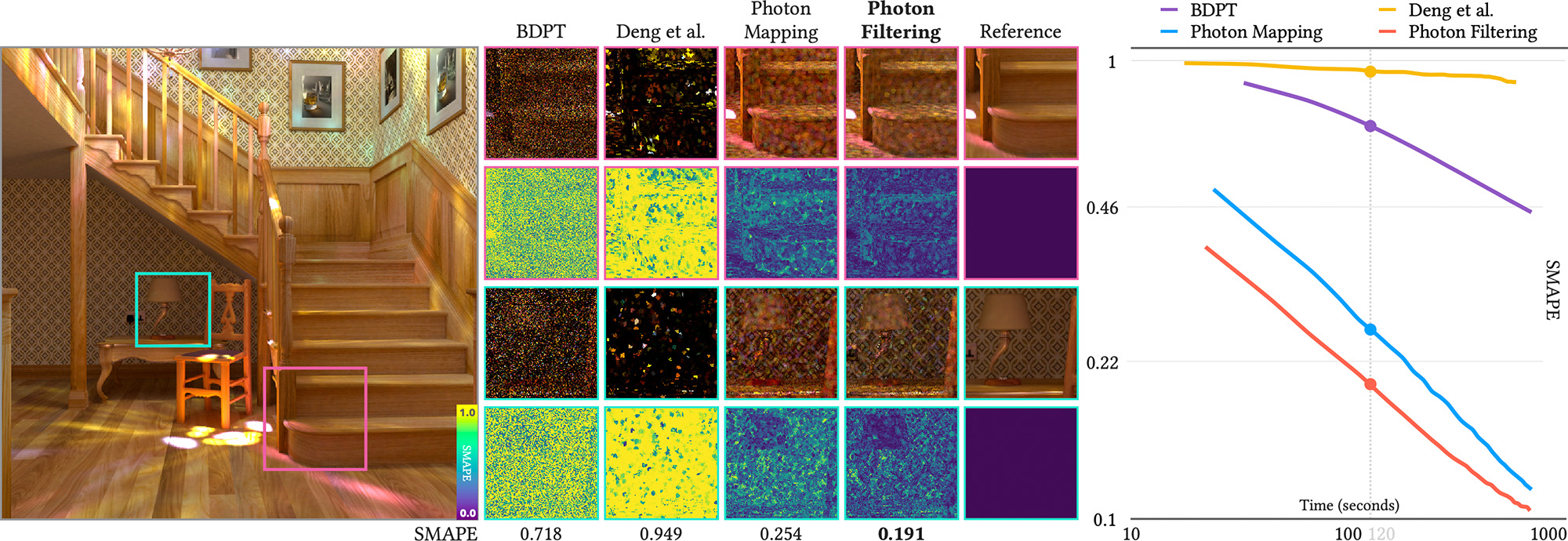
We apply our marginal MIS formulation to light-transport simulation to demonstrate its utility. We devise a marginal path sampling framework that makes previously intractable sampling techniques practical and significantly broadens the path-sampling choices beyond what is presently possible. We highlight results from two algorithms based on marginal MIS: a novel formulation of path-space filtering at multiple vertices along a camera path and a similar filtering method for photon-density estimation.
Downloads and links
- paper (PDF, 9 MB)
- supplemental document (PDF, 9.4 MB)
- fast-forward video (MP4, 2.5 MB)
- talk video (MP4, 52 MB)
- citation (BIB)
Media
Fast-forward video
Talk video
BibTeX reference
@inproceedings{West:2022:MarginalMIS,
author = {Rex West and Iliyan Georgiev and Toshiya Hachisuka},
title = {Marginal multiple importance sampling},
booktitle = {ACM SIGGRAPH Asia 2022 Conference Proceedings},
year = {2022},
doi = {10.1145/3550469.3555388},
isbn = {978-1-4503-9470-3/22/12}
}