Multiple importance sampling for stochastic gradient estimation
Abstract
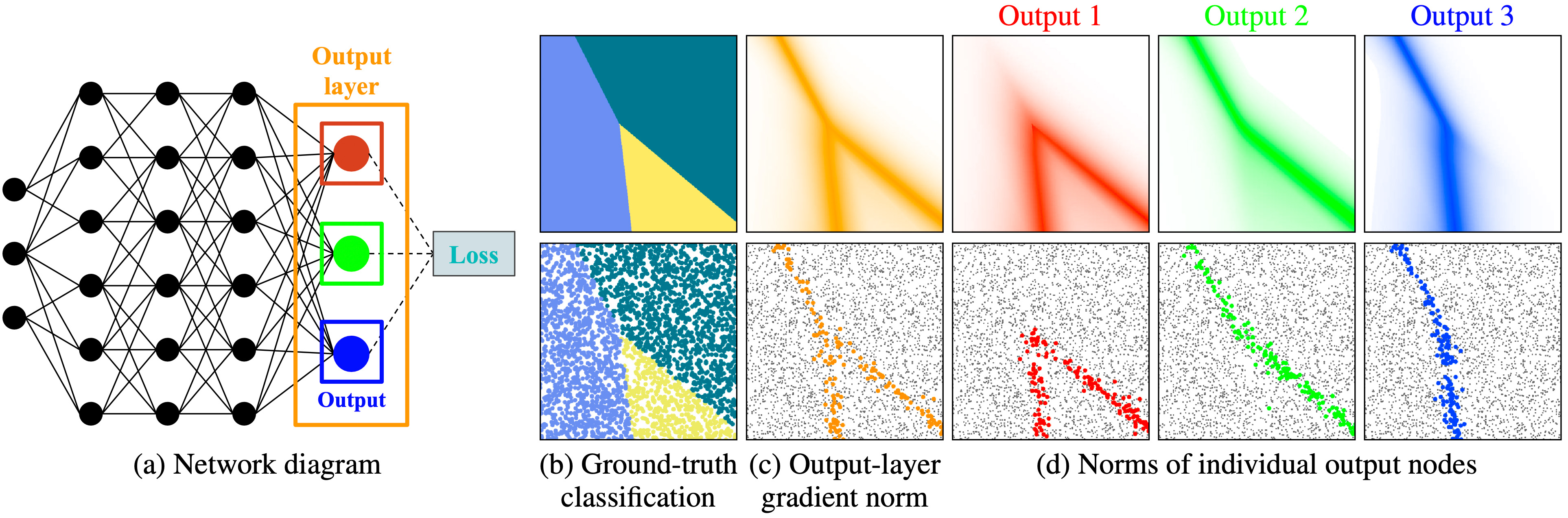
We introduce a theoretical and practical framework for efficient importance sampling of mini-batch samples for gradient estimation from single and multiple probability distributions. To handle noisy gradients, our framework dynamically evolves the importance distribution during training by utilizing a self-adaptive metric. Our framework combines multiple, diverse sampling distributions, each tailored to specific parameter gradients. This approach facilitates the importance sampling of vector-valued gradient estimation. Rather than naively combining multiple distributions, our framework involves optimally weighting data contribution across multiple distributions. This adapted combination of multiple importance yields superior gradient estimates, leading to faster training convergence. We demonstrate the effectiveness of our approach through empirical evaluations across a range of optimization tasks like classification and regression on both image and point cloud datasets.
Downloads and links
- paper (PDF, 1.3 MB)
- Arxiv preprint
- slides – from the conference presentation (PPTX, 5.2 MB)
- citation (BIB)
BibTeX reference
@inproceedings{Salaun:2025:GradientMIS,
author = {Corentin Salaün and Xingchang Huang and Iliyan Georgiev and Niloy Mitra and Gurprit Singh},
title = {Multiple importance sampling for stochastic gradient estimation},
booktitle = {ICPRAM},
year = {2025}
}